Multi-pitch Analysis

What is it?

Multi-pitch analysis is the task of analyzing the pitch content (fundamental frequencies, F0s) of polyphonic audio (e.g. polyphonic music, multi-talker speech, multi-bird songs). It includes estimating the frequency and number of pitches at each time frame, and organizing the pitches according sources. The task is extremely challenging and existing methods do not match human ability in either accuracy or flexibility.

What is it good for?

Multi-pitch analysis is a fundamental problem in computer audition and audio signal processing. In music information retrieval, it is of great interest to researchers working in automatic music transcription, source separation, melody extraction, etc. In speech processing, it is helpful for multi-talker speech recognition and prosody analysis. It is also a step towards approaching the cocktail party effect.

Three levels of multi-pitch analysis

According to MIREX , an annual evaluation campaign for Music Information Retrieval (MIR) algorithms, multi-pitch analysis can be addressed at three levels.

Level 1 (easiest) - Multi-pitch Estimation is to collectively estimate pitch values of all concurrent sources at each individual time frame, without determining their sources.

Level 2 (intermediate) - Note Tracking is to estimate continuous pitch segments that typically correspond to individual notes or syllables. Note that each pitch contour comes from one source but each source can have many contours (e.g. one contour per musical note or spoken word).

Level 3 (hardest) - Multi-pitch Estimation and Streaming is to estimate pitches and stream them into a single pitch trajectory over an entire conversation or music performance for each of the concurrent sources. The trajectory is much longer than those estimated at the second level, and contains a number of discontinuities that are caused by silence, non-pitched sounds and abrupt frequency changes. This level is also called timbre tracking.

Our approach

We propose a system that peforms multi-pitch analysis at the most difficult level, shown in the figure below. The system consists of two stages: The first stage is multi-pitch estimation (gets to Level 1) and the second stage is multi-pitch streaming (gets to Level 3).


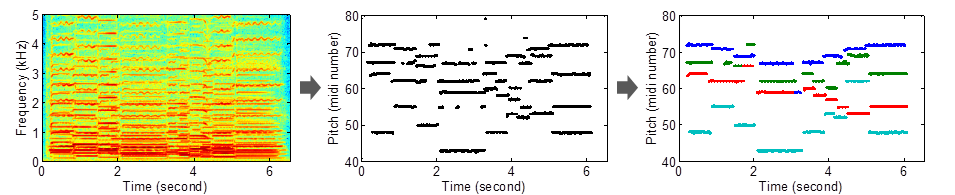
Figure 1. The proposed multi-pitch analysis system: Spectrogram -> Multi-pitch Estimation Results -> Multi-pitch Streaming Results.

Stage 1: Multi-pitch Estimation

Approach

For Multi-pitch estimation, we propose a maximum likelihood approach, where the power spectrum of a time frame is the observation and the pitches are the parameters to be estimated. The likelihood model is defined on both the spectral peaks and non-peak regions (frequencies further than a musical quarter tone from all observed peaks). The peak likelihood and the non-peak region likelihood act as a complementary pair. The former helps find pitches that have harmonics that explain peaks, while the latter helps avoid pitches that have harmonics in non-peak regions. Parameters of these models are learned from thousands of randomly-mixed block chords with different polyphony. We propose an iterative greedy search strategy to estimate the pitches one by one, to avoid the combinatorial problem of concurrent pitch estimation. We also propose a polyphony estimation method to terminate the iterative process. Finally, we propose a post-processing method to refine polyphony and pitch estimates using neighboring frames. <code>

Results of Multi-pitch Estimation

Here is an example of "Ach Gott und Herr", a piece of four-part J.S. Bach chorale, from the Bach10 dataset. This piece is played by violin, clarinet, saxophone and bassoon. <WAV> <Score>


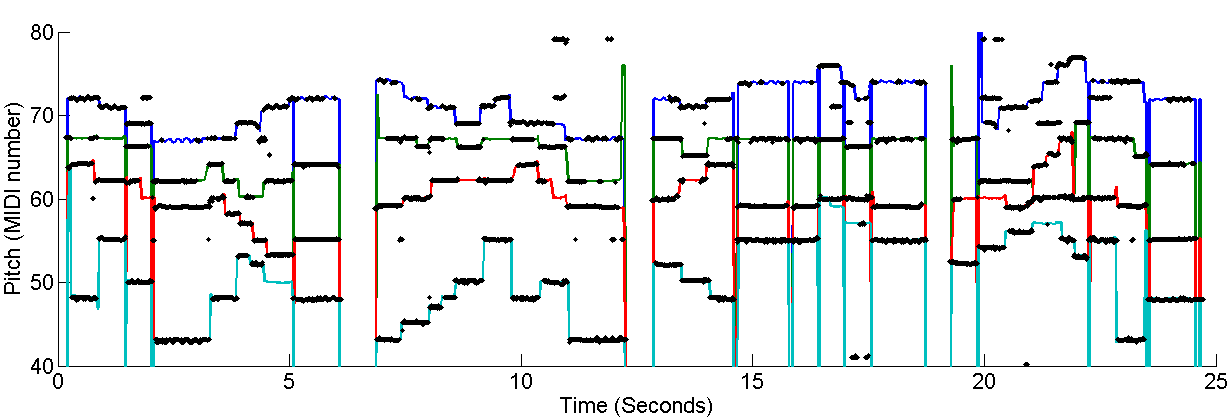
Figure 2. Ground-truth pitches (colored lines) and estimated pitches (black dots) of "Ach Gott und Herr".

 

Figure 3 shows boxplots of comparison results with two state-of-the-art systems on the Bach10 dataset.

Each box represents 330 data points and each point corresponds to 1 second of audio. Higher values are better. The lower and upper lines of each box show 25th and 75th percentiles of the sample. The line in the middle of each box is the sample median, which is also presented as the number below each box. The lines extending above and below each box show the extent of the rest of the samples, excluding outliers. "Mul-F0" measures the overall accuracy of all pitches. "Pre-F0" measures the accuracy of the first pitch found. "Poly known" and "Poly unknown" indicates whether the polyphony informaiton is told to the algorithms or not.


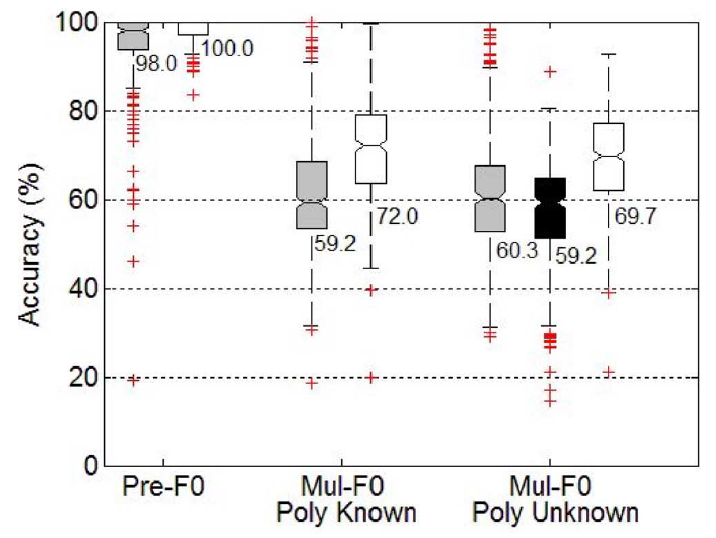
Figure 3. Multi-pitch estimation results comparisons.

Figure 4 shows polyphony estimation histogram on 1000 musical chords of each polyphony. These chords were generated by mixing monophonic notes from the Iowa instrument note sample data set. Musical chords of polyphony 2, 3, and 4 were generated from commonly used note intervals. Triads were major, minor, augmented, and diminished. Seventh chords were major, minor, dominant, diminished, and half-diminished. Musical chords of polyphony 5 and 6 were all seventh chords, so there were always octave relations in each chord. The asterisk indicates the true polyphony.


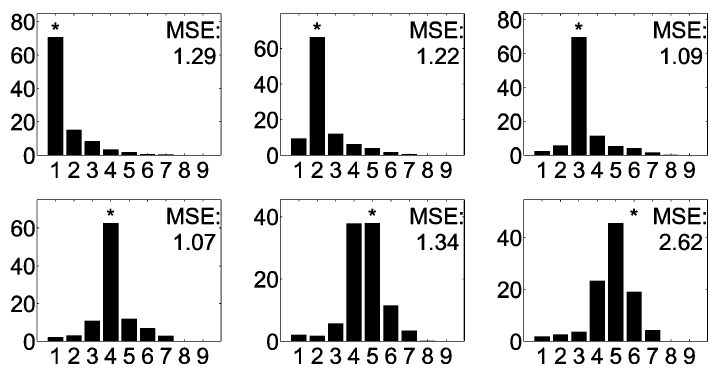
Figure 4. Polyphony estimation results.

Stage 2: Multi-pitch Streaming

Streaming by Constrained Clustering

Given pitches estimates in individual frames, we view the pitch streaming problem as a clustering problem. The instances are the pitch estimates, and each cluster corresponds to a source. Inspired by the fact that human use timbral information to follow a sound source, we define the clustering objective as minimizing the timbral inconsistency within each cluster. Therefore, we need a timbral feature vector for each pitch estimate. We explore several kinds of timbral features. For musical instruments, we showed in a previous paper (DuanEtal'08) that harmonic structure (relative log-amplitudes of harmonics) is an appropriate feature. For speech talkers, we explore MFCC and Uniform Discrete Cepstrum (UDC) features. The MFCC feature is calculated from the separated signal of each talker, after a simple (but inaccurate) source separation step of the mixture audio frame. The UDC feature is what we newly proposed. It can be calculated from several isolated spectral points in the mixture signal, without requiring source separation. <code>

Then the clustering can be done by K-means. However, results are not good. Figure 4 gives an example. This is a duet of saxophone (red circles) and bassoon (black dots). In the streaming results, we can see that a number of pitches are clustered into wrong trajectories. For example, the pitches around MIDI number 55 from 14.8sec to 15.8sec are played by the bassoon but are assigned to both instruments. Another example, from 16.8sec to 17.6sec of the resulted clustering,the saxophone performs two pitches simultaneously. This is not reasonable, since saxophone is a monophonic instrument.

The first error should not be too hard to remove, if we assume that pitches form a continuous contour come from the same source. The second error can also be removed if we do not allow simultaneous pitches to be in the same cluster. Therefore, we add two kinds of constraints to the clustering problem:

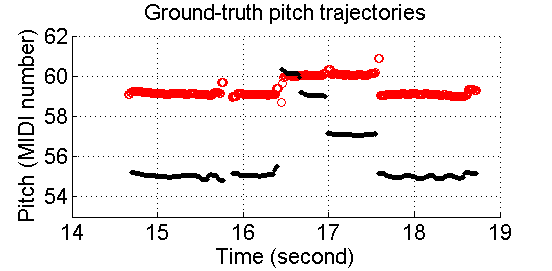
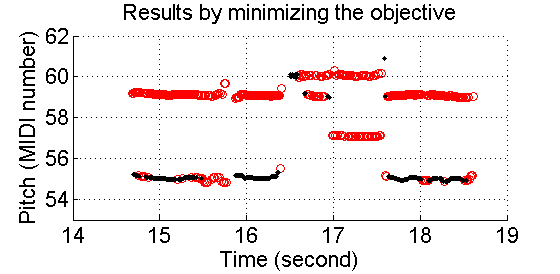Figure 4. Timbral information is not enough to achieve good pitch streaming.

A Novel Constrained Clustering Algorithm

The constrained clustering problem formulated above has the following properties, which make existing algorithms do not apply:

We propose a novel constrained clustering algorithm, which monotonically decreases the objective function, and incrementally satisfy more constraints. More specifically, we start from an initial clustering which only satisfies a subset of all the constraints. Then in each iteration, we update the clustering to a new clustering which strictly decreases the timbral objective function, and also satisfies the constraints that are already satisfied by the old clustering. We then find which (if any) constraints that are satisfied by the new clustering but not the old clustering. We add those constraints to update te set of satisfied constraints. In this way, the objective function strictly monotonically decreases, and the set of satisfied constraints (non-strictly) monotonically expands.

Results of Multi-pitch Streaming

Here is the same example of "Ach Gott und Herr" shown in Figure 1, a piece of four-part J.S. Bach chorale, from the Bach10 dataset. This piece is played by violin, clarinet, saxophone and bassoon. <WAV> <Score>


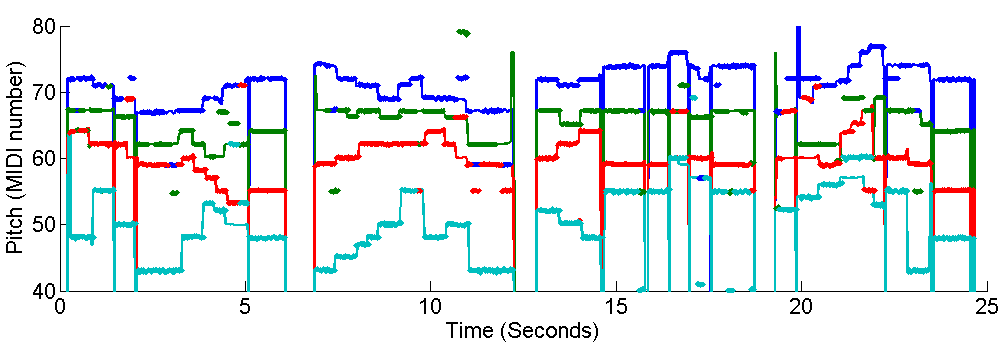
Figure 5. Ground-truth pitches (colored lines) and estimated & streamed pitches (colored dots) of "Ach Gott und Herr".

 

Related Papers

[1] Zhiyao Duan, Bryan Pardo and Changshui Zhang, Multiple fundamental frequency estimation by modeling spectral peaks and non-peak regions, IEEE Trans. Audio Speech Language Process., vol. 18, no. 8, pp. 2121-2133, 2010. <pdf>

[2] Zhiyao Duan, Jinyu Han and Bryan Pardo, Harmonically informed multi-pitch tracking, in Proc. International Society on Music Information Retrieval conference (ISMIR), 2009, pp. 333-338. <pdf> <slides>

[3] Zhiyao Duan, Jinyu Han and Bryan Pardo, Song-level multi-pitch tracking by heavily constrained clustering, in Proc. IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), 2010, pp. 57-60. <pdf> <slides>

[4] Zhiyao Duan, Jinyu Han and Bryan Pardo, Multi-pitch streaming of harmonic sound mixture, IEEE Trans. Audio Speech Language Process., accepted. <pdf>