Don't look back: A novel online music beat tracking method

DON’T LOOK BACK: AN ONLINE BEAT TRACKING METHOD USING RNN AND ENHANCED PARTICLE FILTERING

Overview

Online beat tracking (OBT) has always been a challenging task. Due to the inaccessibility of future data and the need to make inferences in real-time, it is more difficult than offline beat tracking. We propose Don’t Look back! (DLB), a novel approach optimized for efficiency when performing online beat tracking.

Related Work

Most existing online beat tracking methods either apply some offline approaches to a moving window containing past data to make predictions about future beat positions or must be primed with past data at startup to initialize. Figure 1 shows the mechanism of the moving window approach for online beat tracking. This approach has many downsides, for example:

· They require some initialization time to construct the first window. In other words, they don’t give any output until the first window is constructed.

· They suffer from discontinuity and potentially computational overload

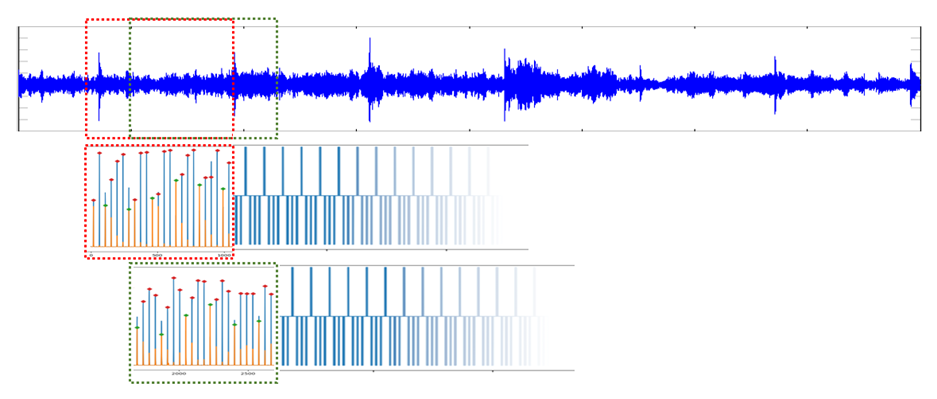
Fig. 1: Moving window strategy for upcoming beat/downbeat estimation

Our approach

DLB feeds the activations of a unidirectional RNN into an enhanced Monte-Carlo localization model to infer beat positions. Without waiting at the beginning to receive a chunk, it provides an immediate beat tracking response, which is critical for many online beat tracking applications. It consists of two main parts. The first one includes a unidirectional pre-trained RNN that delivers the beat activations as each frame's observation likelihood. The second part is a causal sequential Monte Carlo particle filtering that infers beats based on the given state-space, transition model, and observed activations. Fig.2 is the overall scheme of our model.

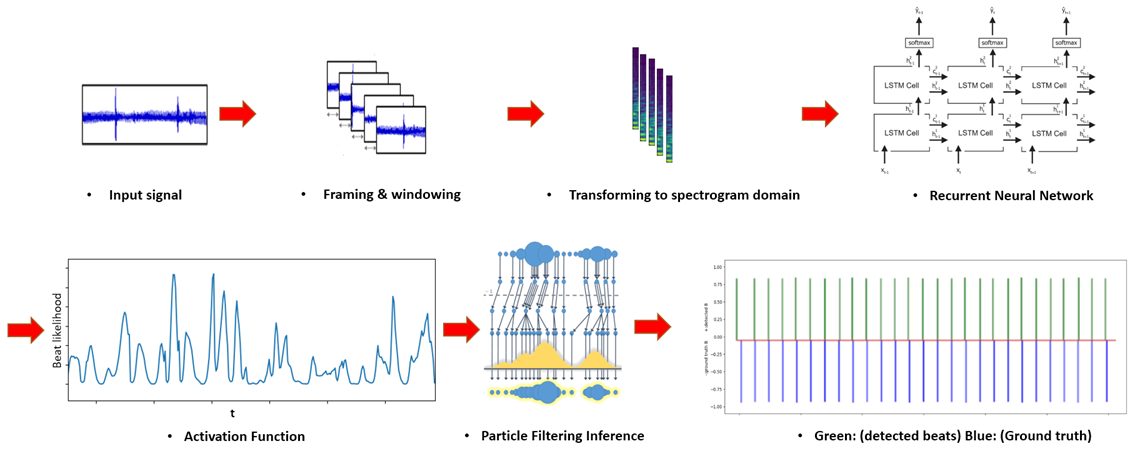
Fig. 2: The block diagram of the proposed online beat tracking method

We approach the problem from the PF localization perspective, which comprises two motion and correction steps. According to the importance sampling principle, a high dimensional probability distribution can be represented by a large number of independent samples from a known arbitrary proposal distribution. We utilize several particles (hypotheses) as beat location candidates and update their state based on the motion model and observation probabilities. In simple words, to obtain the beat positions, first, we distribute the particles uniformly in our state space (which will be explained later in this article), then at each iteration, we take the following steps:

1- Sample particles from proposal distribution which in our case is transition probability. (motion)

2- Compute the new importance weights (4) based on observation probability derived from LSTM Beat activations.

3- Resample based on new normalized weights that discard unlikely hypotheses and generate more rational ones. (correction)

4- Take the median of the positions of all particles and classify the frame as beat if it is within the beat boundary and is far from previous beat with a dynamic time threshold equal to half of the median of all particle’s tempo.

Due to the importance of the speed, we utilized an efficient state space that is an enhanced version of the discrete beat pointer model and requires a way smaller number of particles. Also, the transition model needs sampling only at certain frames. On top of that, we introduced a new observation model, which increases the performance by far. Figure 3 shows our state space.

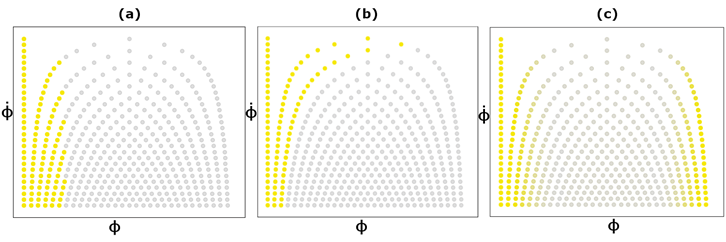
Fig. 3: The state space, including beat states (blue dots) and non-beat states (grey dots)

At fig.3, the vertical axis represents the tempo states by including different integer jumping intervals between adjacent states. The horizontal axis represents the phase of the frame in the beat interval. The grey dots are non-beat stats, and the yellow dots are the beat positions in different investigated setups [vertical line boundary, equal beat states for each row, Gaussian soft transition between beat/non-beat states]. Finally, the figure 4 shows the performance of our model through different iterations.

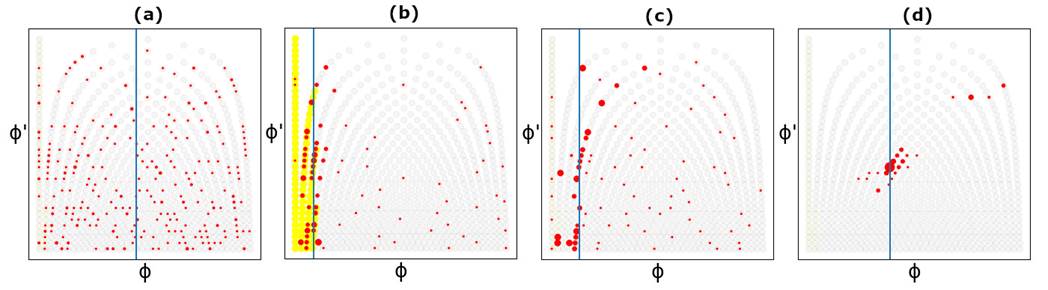
Fig. 4: Proposed PF inference process. (a): particles are initialized randomly and start to move right one step per frame (b): particles within the beat boundary gain weight while many others get discarded, when the first strong beat activation arrives. (c): significant gatherings move right with different paces. (d): Upon the next beat activation’s arrival, many gatherings are discarded and the one with the correct tempo survives; a few double tempo investigators are also added. Blue line is the median of particles’ positions.

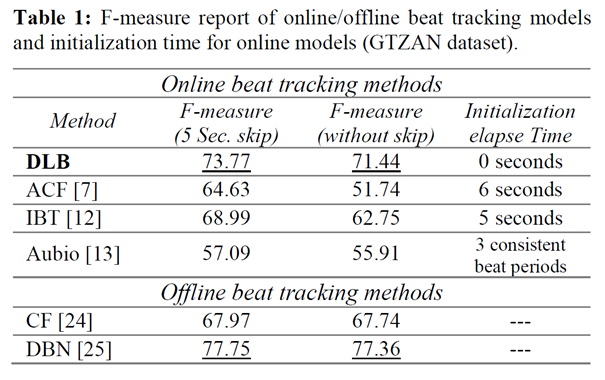
EVALUATION

Here is the F-measure table of the proposed model versus other online beat tracking methods. To compare the performances of our inference model versus offline non-causal inference models, two offline methods are reported as well. As exhibited in table 1, our proposed method significantly outperforms the state-of-the-art online beat tracking methods. Furthermore, its response is immediate, and it doesn’t require an initialization window.





A short video demo of the performance of our method: https://www.youtube.com/watch?v=u2Ee6WsNzoU

((To learn more about this work and further details, please visit our original ICASSP 2021 paper named “DON’T LOOK BACK: AN ONLINE BEAT TRACKING METHOD USING RNN AND ENHANCED PARTICLE FILTERING” from the link down below))

Arxiv link: https://arxiv.org/abs/2011.02619